LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

NAMA : QEZHIA GRACIA AUDREY SONY

KELAS : X MIPA 1


Luas Segi n Beraturan dan Keliling Beserta Contoh Soal

Secara umum pengertian segi n beraturan ialah segi banyak yang memiliki sisi semuanya dengan panjang sama dan besar semua sudutnya sama. Adapun contoh segi n beraturan tersebut yaitu segi sepuluh beraturan, segi enam beraturan, segidelapan beraturan dan lain lain.

1. Luas Bangun Datar Segi n Beraturan

Untuk menghitung luas pada segi n beraturan dapat dilakukan dengan menggunakan rumus luas segitiga dengan aturan sinus di dalamnya. Adapun rumus segitiganya yaitu meliputi:

Luas Segitiga = ½.r.r.sin θ = ½ r² sin 360°/n

Rumus luas segitiga menggunakan aturan sinus di atas dapat digunakan untuk menghitung luas pada segi n beraturan. Adapun rumus luas segi n beraturan yaitu sebagai berikut:

Luas segi n = n × Luas Segitiga
Luas segi n = n/2 r² sin 360°/n


2. Keliling Bangun Datar Segi n Beraturan

Selain rumus luas bangun datar segi n beraturan di atas, adapula rumus keliling segi n beraturan. Panjang segi n (x) dapat dihitung menggunakan aturan kosinus. Panjang x menurut aturan kosinus dalam segitiga PRQ dapat dihitung dengan persamaan seperti di bawah ini:


Dari persamaan di atas dapat diperoleh rumus keliling segi n beraturan seperti di bawah ini:


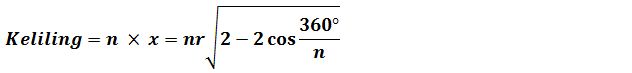
Keterangan:
θ = Sudut pusat yang besarnya 360º/n


3. Contoh Soal Luas dan Keliling Segi n Beraturan
Tentukan luas dan keliling segi enam beraturan yang jari jarinya memiliki panjang 20 cm?

Pembahasan.
Contoh soal tersebut dapat diselesaikan dengan rumus segi n beraturan seperti di bawah ini:
n = 6 (karena bentuknya segienam)
r = 20 cm

Sehingga,
Luas segienam = n/2 r² sin 360°/n
= 6/2 20² sin 360°/6
= 600 sin 60
= 600 ½√3
= 300√3 cm²

Keliling = nr √(2 – 2 cos 360°/n)
=6.20 √(2 – 2 cos 360°/6)
= 120 √(2 – 2.½)
= 120 √(2 -1)
= 120 √1
= 120 cm
Jadi luas dan keliling segi enam beraturan 300√3 cm² dan 120 cm.


Jari-jari Lingkaran Luar dan Dalam Segitiga


1. Lingkaran Dalam Segitiga







Jari-Jari Lingkaran Dalam

Perhatikan gambar di atas, jari-jari lingkarang yang akan kita cari adalah OE = OF = OD. Ketiganya sama dengan tinggi dari segitiga 1, 2 da 3.

Luas Segitiga Besar = Luas ΔI + Luas ΔII + Luas ΔIII

——————- = 1/2 (AB x OD) + 1/2 ( CB x OE) + 1/2 (AC x OF)

——————- = 1/2 (AB x r) + 1/2 (CB x r) + 1/2 (AC x r)

——————- = 1/2 r (AB + CB + C)

——————- = 1/2. r. Keliling Segitiga (setengah keliling bisa dilambangkan dengan s?)

——————- = r. S

Jadi

L = r . S

r = L/S

jadi, jari-jari lingkaran dalam dapat dicari dengan membagi luas segitiga dengan 1/2 kelilingnya. Sekarang yang menjadi masalah adalah bagaimana mencari luas segitiganya? Karena segitiga di atas adalah segitiga sembarang maka bisa menggunakan rumus


Jadi rumus jari-jari lingkaran dalam menjadi:



dengan
L = Luas Segitiga
S = 1/2 keliling Δ = 1/2 (a+b+c)

Rumus di atas tergantung jenis segitiga. Kalau segitiga siku-siku akan lebih enak mencari luasnya dengan rumus 1/2 alas kali tinggi daripada menggunakan s.
Lingkaran Luar Segitiga

Lingkaran luar segitiga adalah lingkran yang dibentuk dari perpanjangan garis bagi tiga sisi segitiga dan kelilinya akan tepat menyinggung tiga titik sudut segitiga yang ada di dalamnya. Perhatikan gambar di bawah ini



Pada gambar diatas, terdapat sebuah segitiga ABC dengan dengan sisi a,b, dan c. Ada lingkaran luar yang berpusat di titik O yang mengitari segitiga tersebut. OA, OB, OC. dan OD masing-masing adalah jari-jari lingkaran luar yang akan kita cari rumusnya. Untuk membantu menemukan rumus jari-jari, kita memakai garis bantu yaitu garis tinggi segitiga CT dan garis diameter yang ditarik dari titik C (garis CD).

Coba perhatikan ΔCAD dengan ΔCTB

∠CAD = ∠CTB = 90o (ingat sifat sudut keliling yang menghadap diameter sama dengan 90º)

∠ADC = ∠TBC (ingat bahwa dua sudut keliling yang menghadap busur lingkaran yang sama adalah sama besar)

Karena ada dua pasang sudut yang sama maka bisa disimpulkan bahwa ΔCAD dan ΔCTB sebagung (kongruen). Karena sebangun maka perbandingan sisi-sisinya akan sama.

BC/CD = CT/AC
CD (diameter) = BC x AC / CT
CD (diameter) = a x b / CT……. (persamaan 1)

Nilai CT bisa kita cari dengan persamaan Luas

Luas ΔABC = 1/2 AB x CT
2 Luas ΔABC = AB x CT
CT = 2 Luas ΔABC / AB
CT = 2L/ c……..(persamaan 2)

Kita masukkan persamaan 2 ke persamaan 1

CD = a x b / CT
CD = a x b / (2L/c)
CD = a x b x c / 2L

Jari-jari = 1/2 CD
r = 1/2 CD = a x b x c / 4L



a,b,dan c = sisi-sisi segitiga

L = luas segitiga

GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

Garis singgung lingkaran persekutuan dalam melibatkan dua lingkaran dan sebuah garis singgung lingkaran. Untuk lebih jelasnya dapat dilihat pada gambar di bawah.


Dari gambar di atas, bisa kita simpulkan bahwa:

Titik pusat lingkaran besar adalah M dengan jari jari R.

Titik pusat lingkaran kecil adalah N dengan jari-jari r.

Garis singgung persekutuan dalam adalah AB = d

Jarak titik pusat kedua lingkaran besar dan kecil adalah MN = p

Jika garis AB digeser ke atas dari titik B ke N maka akan diperoleh garis ON.

Garis ON sejajar AB, sehingga sudut MON sama besar dengan sudut MAB, yaitu siku-siku (90 derajat )

Lalu sekarang fokus ke persegi panjang ABNO,

Garis AB sejajar dengan NO, AO sejajar dengan BN, yang berarti sudut MON sama dengan sudut MAB, yaitu siku-siku (90 derajat)

Jadi, segi empat ABNO merupakan persegi panjang dengan panjang AB = d, dan lebar BN = r.

Sekarang lihat lagi segitiga MNO, yang merupakan segitiga siku-siku dengan sudut siku-siku di titik O. Maka dengan menggunakan rumus pythagoras, akan diperoleh

ON2 = MN2 – MO2

ON =

Lalu, karena panjang AO sama dengan panjang BN, maka MO = R + r.

Oleh karena itu, bisa disimpulkan bahwa rumus panjang garis singgung persekutuan dalam dua lingkaran (d) adalah

Contoh soal:

Diketahui panjang jari-jari dua buah lingkaran masing-masing adalah 5 cm dan 2 cm. Jarak kedua titik pusatnya adalah 25 cm. Hitunglah panjang garis singgung persekutuan dalam kedua lingkaran tersebut!

Jawab:

Masukkan rums d yang sudah dijelaskan diatas tadi:

Maka panjang garis singgung dalam kedua lingkaran tersebut adalah 24 cm.
Menentukan Panjang Garis Singgung Persekutuan Luar Dua Lingkaran

Sama seperti garis singgung persekutuan dalam dua lingkaran, garis singgung persekutuan luar dua lingkaran juga melibatkan dua buah lingkaran dan sebuah garis singgung. Bedanya ada di posisi garis singgung lingkaran. Dua titik singgung lingkaran pada garis singgung persekutuan dalam dua lingkaran terletak bersebrangan, sedangkan dua titik singgung lingkaran pada garis singgung persekutuan luar dua lingkaran terletak di sisi yang sama. Untuk lebih jelasnya, coba lihat gambar dibawah ini:

Dari gambar di atas, dapat disimpulkan bahwa:

Titik pusat lingkaran besar adalah M dengan jari-jari R.

TItik pusat lingkaran kecil adalah N denga jari jari r.

Garis singgung persekutuan luar adalah AB = f

Jarak titik pusat kedua lingkaran adalah MN = p.

Jika garis AB kita geser sejajar ke bawah dari B ke N, maka akan diperoleh garis ON.

Garis AB sejajar ON, sehingga sudut MON sama dengan sudut MAB yaitu 90o (siku-siku).

Sekarang coba lihat persegi panjang ABNO. Garis AB sejajar dengan ON, dan garis AO sejajar dengan garis BN.

Karena panjang ON sama dengan AB dan MO = R – r, maka rumus panjang garis singgung persekutuan luar dua lingkaran (f) adalah

Contoh soal:

Diketahui panjang jari-jari dua lingkaran masing-masing adalah 15 cm dan 5 cm. Panjang garis singgung persekutuan luar kedua lingkaran adalah 24 cm. Hitunglah jarak kedua titik pusat kedua lingkaran tersebut!

Jawab:





Maka, jarak kedua titik pusatnya = 26 cm


Daftar Pustaka

https://rpp.co.id/rumus-soal-luas-keliling-segi-n-beraturan/

https://rumushitung.com/2014/12/22/rumus-jari-jari-lingkaran-dalam-dan-lingkaran-luar-segitiga/

https://www.zenius.net/blog/rumus-garis-singgung-lingkaran